The OGC defines properties that describe
-
Characteristics of spatial objects
-
Spatial relationships that can exist among objects
Vertica provides functions that test for and analyze the following properties and relationships.
This is the multi-page printable view of this section. Click here to print.
The OGC defines properties that describe
Characteristics of spatial objects
Spatial relationships that can exist among objects
Vertica provides functions that test for and analyze the following properties and relationships.
The set of points that define the limit of a spatial object:
Points, multipoints, and geometrycollections do not have boundaries.
The boundary of a linestring is a multipoint object. This object contains its start and end points.
The boundary of a multilinestring is a multipoint object. This object contains the start and end points of all the linestrings that make up the multilinestring.
The boundary of a polygon is a linestring that begins and ends at the same point. If the polygon has one or more holes, the boundary is a multilinestring that contains the boundaries of the exterior polygon and any interior polygons.
The boundary of a multipolygon is a multilinestring that contains the boundaries of all the polygons that make up the multipolygon.
The set of all points that are within or equal to a specified distance from the boundary of a spatial object. The distance can be positive or negative.
Positive buffer:

Negative buffer:
One spatial object contains another spatial object if its interior includes all points of the other object. If an object such as a point or linestring only exists along a polygon's boundary, the polygon does not contain it. If a point is on a linestring, the linestring contains it; the interior of a linestring is all the points on the linestring except the start and end points.
Contains(a, b) is spatially equivalent to within(b, a).
The smallest convex polygon that contains one or more spatial objects.
In the following figure, the dotted lines represent the convex hull for a linestring and a triangle.

Two spatial objects cross if both of the following are true:
The two objects have some but not all interior points in common.
The dimension of the result of their intersection is less than the maximum dimension of the two objects.
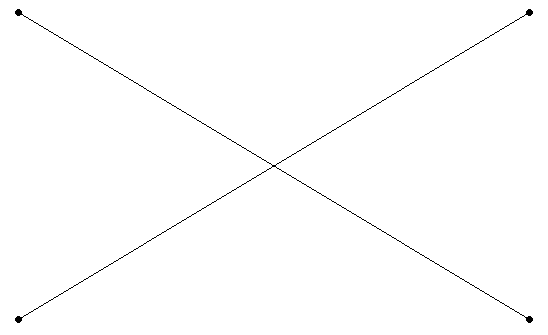
Two spatial objects have no points in common; they do not intersect or touch.
The minimum bounding rectangle that contains a spatial object.
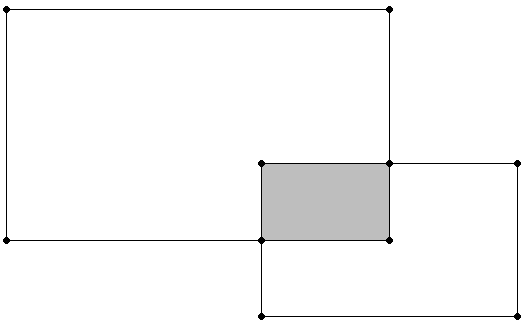
The envelope for the following polygon is represented by the dotted lines in the following figure.

Two spatial objects are equal when their coordinates match exactly. Synonymous with spatially equivalent.
The order of the points do not matter in determining spatial equivalence:
LINESTRING(1 2, 4 3) equals LINESTRING(4 3, 1 2).
POLYGON ((0 0, 1 1, 1 2, 2 2, 2 1, 3 0, 1.5 –1.5, 0 0)) equals POLYGON((1 1 , 1 2, 2 2, 2 1, 3 0, 1.5 –1.5, 0 0, 1 1)).
MULTILINESTRING((1 2, 4 3),(0 0, –1 –4)) equals MULTILINESTRING((0 0, –1 –4),(1 2, 4 3)).
The set of points not contained within a spatial object nor on its boundary.
A set of zero or more objects from any of the supported classes of spatial objects.
The set of points contained in a spatial object, excluding its boundary.
The set of points that two or more spatial objects have in common.
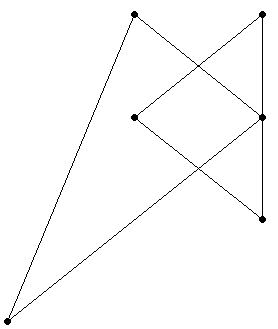
If a spatial object shares space with another object, but is not contained within that object, the objects overlap. The objects must overlap at their interiors; if two objects touch at a single point or intersect only along a boundary, they do not overlap.
When a spatial object is spatially related to another object as defined by a DE-9IM pattern matrix string.
A DE-9IM pattern matrix string identifies how two spatial objects are spatially related to each other. For more information about the DE-9IM standard, see Understanding Spatial Relations.
For points, multipoints, linestrings, or multilinestrings, a spatial object is simple if it does not intersect itself or has no self-tangency points.
Polygons, multipolygons, and geometrycollections are always simple.
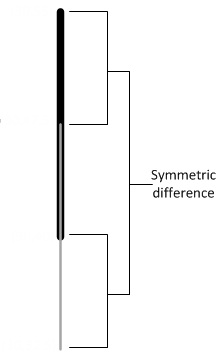
The set of all points of a pair of spatial objects where the objects do not intersect. This difference is spatially equivalent to the union of the two objects less their intersection. The symmetric difference contains the boundaries of the intersections.
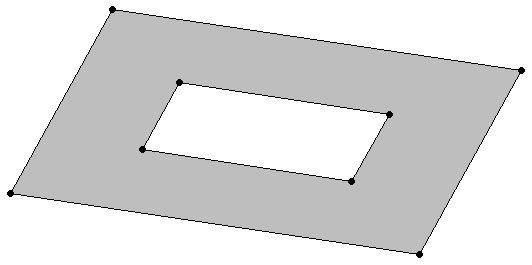
In the following figure, the shaded areas represent the symmetric difference of the two rectangles.

The following figure shows the symmetric difference of two overlapping linestrings.
For two or more spatial objects, the set of all points in all the objects.

For a polygon or multipolygon, when all of the following are true:
It is closed; its start point is the same as its end point.
Its boundary is a set of linestrings.
No two linestrings in the boundary cross. The linestrings in the boundary may touch at a point but they cannot cross.
Any polygons in the interior must be completely contained; they cannot touch the boundary of the exterior polygon except at a vertex.
Valid polygons:

Invalid polygon:

A spatial object is considered within another spatial object when all its points are inside the other object's interior. Thus, if a point or linestring only exists along a polygon's boundary, it is not considered within the polygon. The polygon boundary is not part of its interior.
If a point is on a linestring, it is considered within the linestring. The interior of a linestring is all the points along the linestring, except the start and end points.
Within(a, b) is spatially equivalent to contains(b, a).
